Las curvas de Bézier son una herramienta fundamental en el diseño gráfico y la ingeniería de software, pero ¿alguna vez te has preguntado cómo funcionan realmente? En este post, nos sumergiremos en las matemáticas detrás de estas curvas y exploraremos cómo se aplican en herramientas de modelado como Enterprise Architect.
Las curvas de Bézier fueron desarrolladas por Pierre Bézier en la década de 1960 para el diseño de automóviles. Pierre Étienne Bézier (1910-1999) fue un ingeniero y matemático francés cuyo trabajo revolucionó el diseño industrial y gráfico. Nacido en París, Bézier se graduó de la École Nationale Supérieure d'Arts et Métiers en 1930 y de la École Supérieure d'Électricité en 1931. Pasó la mayor parte de su carrera en Renault, donde comenzó en 1933 y llegó a ser director del departamento de diseño mecánico. Su contribución más significativa fue el desarrollo de las curvas y superficies que llevan su nombre, las curvas de Bézier, inicialmente concebidas para facilitar el diseño de carrocerías de automóviles.
Estas curvas, que permiten describir formas complejas de manera matemática y precisa, se convirtieron en una herramienta fundamental en el diseño asistido por computadora (CAD) y en gráficos por computadora. Aunque no fue el primero en describir estas curvas (Paul de Casteljau había desarrollado un algoritmo similar anteriormente en Citroën), Bézier las popularizó y las aplicó extensamente en la industria. Su trabajo no solo transformó la industria automotriz, sino que también sentó las bases para el desarrollo de software de diseño gráfico moderno, siendo hoy en día un componente esencial en programas como Adobe Illustrator, Photoshop o Gimp.
Matemáticamente, estas curvas son una representación paramétrica de curvas polinómicas. Las curvas de Bézier son curvas paramétricas de segundo grado definidas por tres puntos de control.
Ecuación General
La ecuación para una curva de Bézier cuadrática es:
B(t) = (1-t)²P₀ + 2(1-t)tP₁ + t²P₂
Donde:
- t es un parámetro que varía de 0 a 1
- P₀ es el punto de inicio
- P₁ es el punto de control
- P₂ es el punto final
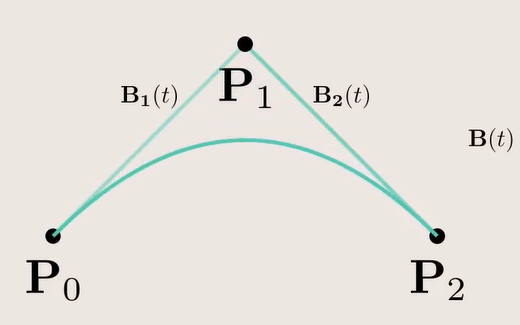
Geométricamente, la curva comienza en P₀, se curva hacia P₁ (sin tocarlo necesariamente), y termina en P₂. El punto P₁ actúa como un "imán" que atrae la curva hacia sí mismo.
Propiedades Matemáticas Clave
- Continuidad: Las curvas de Bézier cuadráticas son continuas y tienen una primera derivada continua, lo que resulta en transiciones suaves, ideales para el diseño gráfico.
- Simetría: Si intercambias P₀ y P₂, obtienes la misma curva pero en dirección opuesta.
- Tangentes: Las tangentes en los puntos extremos (P₀ y P₂) son colineales con los segmentos P₀P₁ y P₁P₂ respectivamente.
Aplicación en Photoshop y otros programas de diseño gráfico
Photoshop utiliza curvas de Bézier cuadráticas en varias de sus herramientas, principalmente en la herramienta Pluma.
La Herramienta Pluma y las Curvas de Bézier
- Haz clic para crear el punto de inicio (P₀)
- Haz clic y arrastra para crear el punto de control (P₁) y el punto final (P₂)
- Photoshop dibuja la curva cuadrática resultante
Ventajas de las Curvas Cuadráticas en Diseño Gráfico
- Simplicidad: Más fáciles de manejar que las curvas cúbicas para principiantes
- Eficiencia: Requieren menos cálculos, lo que es beneficioso para el rendimiento
- Suficiencia: Para muchas aplicaciones de diseño, las curvas cuadráticas son más que adecuadas
Aplicación en Enterprise Architect
Enterprise Architect también permite el uso de curvas de Bézier para crear conectores curvos en diagramas, mejorando la legibilidad y estética de los modelos.
¿Cómo Activar Conectores Curvos en EA?
- Selecciona un conector en tu diagrama
- Haz click derecho
- Selecciona la opción Line Style y luego Bezier

Ventajas de Usar Curvas de Bézier en Diagramas de EA
- Mejora la claridad visual al reducir el cruce de líneas
- Permite representar relaciones de manera más intuitiva
- Facilita la creación de diagramas más compactos y organizados
Las curvas de Bézier son un ejemplo perfecto de cómo un concepto matemático aparentemente simple puede tener un impacto profundo en campos tan diversos como el diseño gráfico y la ingeniería de software. Su elegancia matemática se traduce en herramientas intuitivas y poderosas que utilizamos a diario, quizás sin darnos cuenta.
La próxima vez que estés creando un diagrama en EA, recuerda que detrás de esos suaves conectores curvos hay una rica historia matemática y una ecuación que ha revolucionado el diseño gráfico y la ingeniería de software.
¿Quieres profundizar más en el tema? Te invito a explorar las implementaciones de curvas de Bézier en diferentes lenguajes de programación o a experimentar con herramientas interactivas en línea que te permitan manipular estas curvas en tiempo real.